(R) 밀도함수와 히스토그램 그리기

정규분포 함수 그리기, 값 계산하기

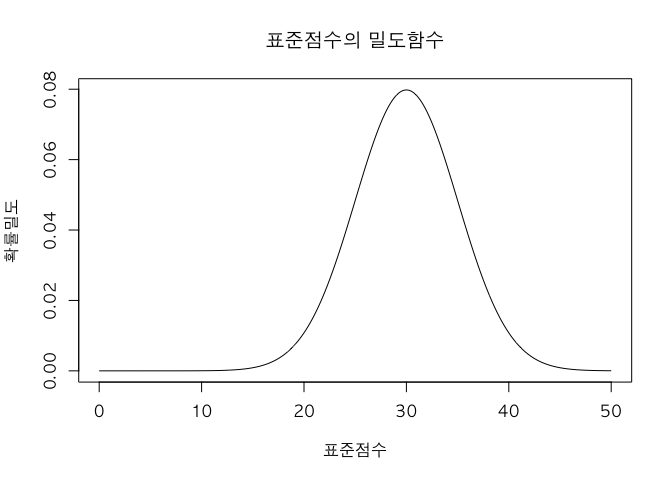
1. 표준점수의 밀도함수를 그려보세요.

표준점수는 m = 30 , sd = 5 인 정규분포를 따른다.

x = seq(0,50,0.1)
y = dnorm(x, 30,5)
plot(x,y, type = 'l', xlab = '표준점수', ylab = '확률밀도', main = '표준점수의 밀도함수')

2. 임의로 1명을 선택하여 통계 점수를 조회했을떄 45점 보다 높은 점수를 받았을 확률

(1-pnorm(45, 30, 5))*100

## [1] 0.1349898

3. 상위 10% 점수를 받았을때 해당 점수는?

qnorm(0.9 ,mean = 30, sd=5)

## [1] 36.40776

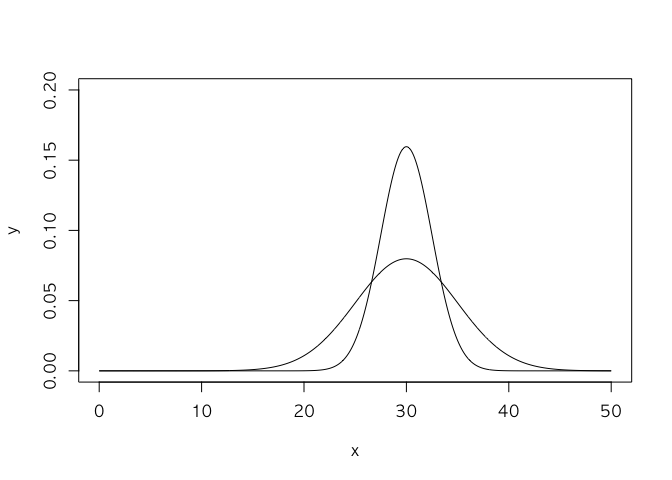
4. 수강생이 16명, 16명 평균을 냈을떄, 이 평균값을 따르는 분포의 확률밀도 함수를 1번의 그래프와 겹쳐 그려보라.

x = seq(0,50,0.1)
y = dnorm(x, 30,5)
plot(x,y, type = 'l', ylim = c(0, 0.2))
x2 <- seq(0,50,0.1)
y2 <- dnorm(x, 30, 5/2)
lines(x2,y2)

5. 수강생의 통계점수의 평균을 내었을떄, 이 값이 38 점보다 높게 나올 확률

(1-pnorm(38, 30, 5/2)) *100

## [1] 0.06871379

카이제곱분포 함수 그리기, 값 계산하기

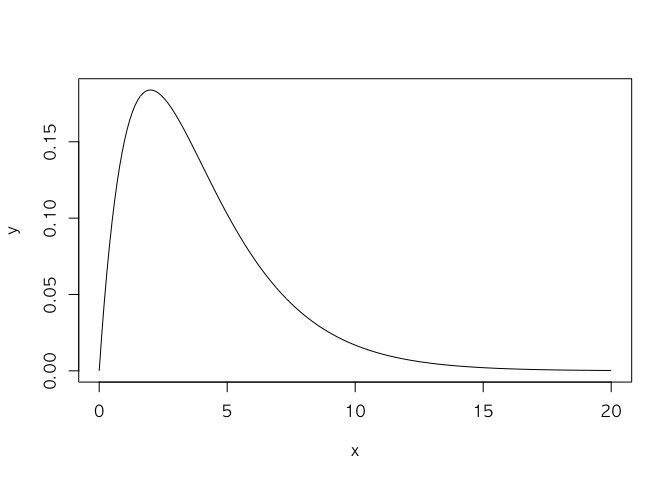
1. 자유도가 4인 카이제곱 분포의 확률밀도함수를 그려보세요.

dchisq, pchisq, qchisq, rchisq
카이제곱 분포는 정의역이 0보다 크거나 같다.

x <- seq(0, 20 , 0.1)
y <- dchisq(x, 4)
plot(x,y, type = 'l')

2. 다음의 확률을 구하세요.

$P(3 \leq X \leq 5)$

pchisq(5, 4) - pchisq(3, 4)

## [1] 0.2705279

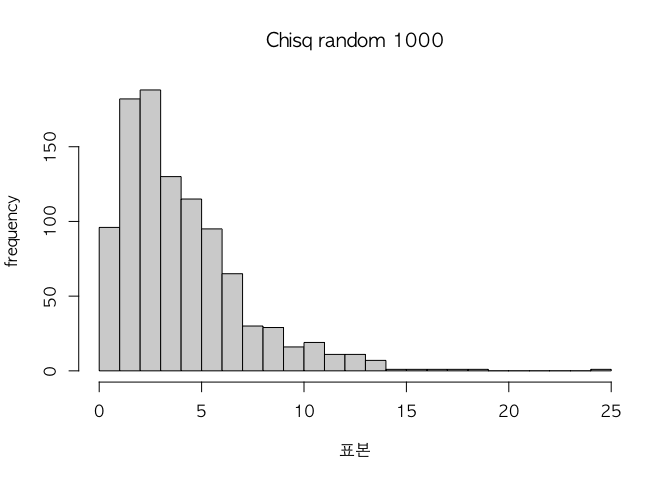
3. 자유도가 4인 카이제곱분포에서 크기가 1000인 표본을 뽑은 후, 히스토그램을 그려보세요.

set.seed(2023)
a <- rchisq(1000,4)
hist(a, breaks = 30,prob = FALSE,  main = 'Chisq random 1000' , xlab = '표본', ylab = 'frequency')

4. 자유도 4인 카이제곱 분포를 따르는 확률변수에서 나올 수 있는 값 중 상위 5%에 해당하는 값은 얼마?

qchisq(0.95, 4)

## [1] 9.487729

5. 3번에서 뽑힌 표본값들 중 상위 5%에 위치한 표본의 값은 얼마인가?

quantile(a, 0.95)

##      95% 
## 10.28894

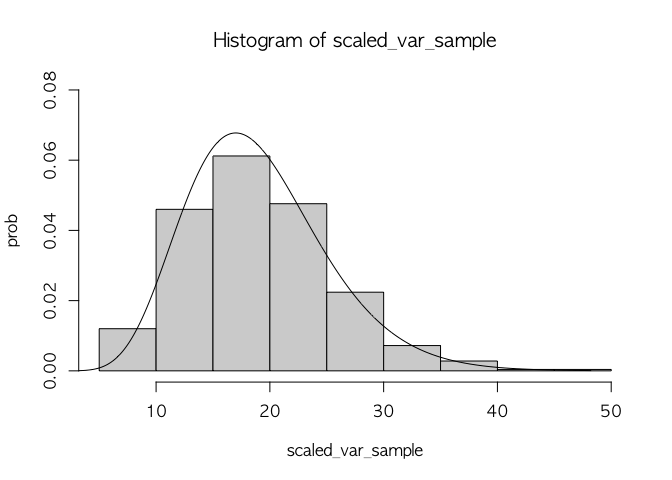
6. 평균이 3 , 표준편차가 2인 정규분포를 따르는 확률변수에서 크기가 20인 표본을 뽑은 후 표본분산을 계산한 것을 $s_1^2$ 이라 생각한다.

같은 방법으로 500개의 $s^2$ 를 발생시킨다.
발생한 500개의 $s^2$ 들 각각에 4.75를 곱하고, 그것들의 히스토그램을 그려라(prob = TRUE).
위에서 그린 히스토그램에 자유도가 19인 카이제곱분포 확률밀도함수를 겹쳐 그려라.

set.seed(2023)

n <- 20
num_sample <- 500 # list 공간 크기
var_sample <- numeric(num_sample) # list 500개 공간 만듦

for (i in 1:num_sample) {
  x <- rnorm(n, 30, 2)
  var_sample[i] <- var(x) # list 에 넣음
}

scaled_var_sample <- var_sample * 4.75

hist(scaled_var_sample, prob = TRUE, ylim = c(0,0.08), ylab = 'prob')

x <- seq(0, max(scaled_var_sample), length.out = 1000)
pdf_chi19 <- dchisq(x, df = 19)
lines(x, pdf_chi19)

신뢰구간 구하기

16명을 무작위로 선별하여 몸무게 측정한 데이터, 이 데이터 이용하여 전체 몸무게 평균을 예측하고자한다. (정규분포를 따른다.)

1. 모평균에 대한 95% 신뢰구간을 구하세요. (모분산을 모를때)

x <- c(71.2,62.2,53.2,70.1,65.7,82.9,62.9,82,68,67.3,75.3,67.9,77.6,78.6,66,79)
mean <- mean(x)
se <- sd(x)/sqrt(16)

lower <- round(mean - qt(0.975, 15)*se, 3)
upper <- round(mean + qt(0.975, 15)*se, 3)

c(lower, upper)

## [1] 66.289 74.948

2. 작년 표준편차는 6이다. 이 정보를 이번년 분포의 표준편차로 대체하여 모평균에 대한 90% 신뢰구간을 구하세요. (모분산을 알때)

모표준편차를 알떄는 t분포가 아니라 z분포(표준정규분포)로 계산한다.

sd_pre <- 6
se_pre <- 6/sqrt(16)

lower_pre <- qnorm(0.05,mean,6/4)
upper_pre <- qnorm(0.95,mean,6/4)

c(lower_pre, upper_pre)

## [1] 68.15147 73.08603