(R) [가설검정] t검정의 가정과 신뢰구간 구하기

신형 자동차의 에너지 소비 효율 등급

표본은 신형 자동차 15대의 복합 에너지 소비 효율을 측정한 결과가 data에 들어가 있다.
평균 복합 에너지 소비 효율이 16이상인 경우 1등급으로 판단할 수 있다.
유의수준 1% 로 1등급으로 판단할 수 있을지 판단하시오.

data <- c(15.078,15.752,15.549,15.56,16.098,13.277,15.462,16.116,15.214,16.93,14.118,14.927,15.382,16.709,16.804)

1. t 검정을 위한 가정체크를 진행하세요.

정규성 검정 방법

1) QQ plot

car::qqPlot(data, distribution = ‘norm’)

# install.packages('car') 필요
car::qqPlot(data, distribution = 'norm')

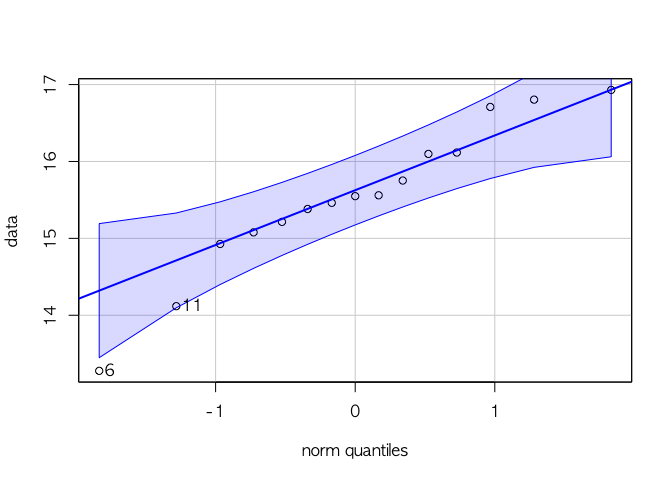
## [1]  6 11

2) Shapiro-Wilk 검정

shapiro.test(data)
귀무가설 : 정규성을 만족한다.

shapiro.test(data)

## 
##  Shapiro-Wilk normality test
## 
## data:  data
## W = 0.94485, p-value = 0.4473

3) Anderson-Darling 검정

ad.test(data)
귀무가설 : 특정분포(정규분포)를 만족한다.
Anderson 검정은 특정분포를 따르는지 검정하는 것이지만, ad.test는 정규분포를 검정하는데 사용된다.

# install.packages('nortest') 필요
library(nortest)
ad.test(data)

## 
##  Anderson-Darling normality test
## 
## data:  data
## A = 0.33106, p-value = 0.4706

4) Kolmogorov-Smirnov 검정

1) one-sample 검정 : data 가 특정분포를 따르는지 검정한다.
ks.test(data, ‘pnorm’, mean(data), sd(mean))
2) two-sample 검정 : 두 데이터가 같은 분포를 따르는지 검정한다.
ks.test(x,y)
귀무가설 : 특정 분포(같은 분포) 를 따른다.

ks.test(data, 'pnorm', mean(data), sd(data))

## 
##  Exact one-sample Kolmogorov-Smirnov test
## 
## data:  data
## D = 0.13532, p-value = 0.9124
## alternative hypothesis: two-sided

2. 검정을 위한 가설을 명확하게 서술하시오.

$H_0$ : 신형 모델의 평균 에너지 소비효율은 16 이상이다. $\bar{X} \geq 16$
$H_A$ : 신형 모델의 평균 에너지 소비효율은 16 미만이다. $\bar{X} < 16$

3. 검정통계량을 계산하시오.

\[\begin{aligned} t = \frac{\bar{X}-\mu_0}{S/\sqrt{n}} \end{aligned}\]

t_value = (mean(data) - 16) / (sd(data)/sqrt(15))
t_value

## [1] -1.850045

4. p-value를 구하시오.

$H_0 : \bar{X} \geq 16$.
$H_A : \bar{X} < 16$
인 단측 검정이므로, $P(\bar{X}<t)$ 값을 p-value로 구한다.

pt(t_value, length(data)-1)

## [1] 0.04276242

5. 주어진 유의수준에 대응하는 기각역은 얼마인가요?

reject <- round(qt(0.01, length(data)-1),3)
reject

## [1] -2.624

$P(\bar{X}< -2.624)$

6. 평균 복합 에너지 소비 효율에 대하여 95% 신뢰구간을 구해보세요.

\[\begin{aligned} \bar{X} + t_{a, n-1}\frac{S}{\sqrt{n}} \leq \mu \end{aligned}\]

lower <- mean(data) + qt(0.05, length(data)-1) * sd(data) / sqrt(length(data)) 
lower

## [1] 15.08593

$\mu \geq 15.0859264$

7. 평균 복합 에너지 소비 효율이 15라면, 위의 검정의 검정력을 구하세요. (단, 검정력 계산시 모분포의 표준편차를 1이라고 가정)

실제 평균 $\mu = 15$ , 실제 표준 편차 $\sigma = 1$
효과 크기(d , Cohen’s d) = $\frac{\mu-\mu_0}{\sigma}$
유의 수준(sig.level) = 0.01 표본 크기(n)

# install.packages('pwr')
library(pwr)
pwr.norm.test(d = (16-15)/1, n = length(data), sig.level = 0.01, power = NULL, alternative = 'greater')

## 
##      Mean power calculation for normal distribution with known variance 
## 
##               d = 1
##               n = 15
##       sig.level = 0.01
##           power = 0.9390244
##     alternative = greater

8. 평균 에너지 소비 효율이 16인지 아닌지를 유의수준 5% 하에서 검정을 진행하려고 한다. (모분포의 표준편차를 2라고 가정) 평균 에너지 소비효율이 15일때, 주어진 검정의 검정력을 구하세요.

모분포의 표준편차를 알고 있기 때문에, t 분포가 아닌 z 분포로 접근해야한다.

d = (16-15)/2
pwr.norm.test(d = d, n = length(data), sig.level = 0.05,power = NULL, alternative = 'two.sided')

## 
##      Mean power calculation for normal distribution with known variance 
## 
##               d = 0.5
##               n = 15
##       sig.level = 0.05
##           power = 0.4906856
##     alternative = two.sided

9. 검정력을 80% 로 만족시키도록하는 표본갯수를 구하세요.

d = (16-15)/2
pwr.norm.test(d = d, n = NULL, sig.level = 0.05, power = 0.8, alternative = 'two.sided')

## 
##      Mean power calculation for normal distribution with known variance 
## 
##               d = 0.5
##               n = 31.39544
##       sig.level = 0.05
##           power = 0.8
##     alternative = two.sided